บทนำ
เคยสงสัยไหมครับว่าโมเดล Machine Learning ที่เราปั้นมากับมือ มีค่า Accuracy สูงลิ่ว แถมค่า AUC ก็สวยสุดๆ แต่พอเอาไปใช้จริง ทำไมธุรกิจกลับไม่ได้กำไรอย่างที่คิด? 🤯
วันนี้ผมจะพาทุกคนไปหาคำตอบของคำถามนี้ ผ่าน Loan Approval Project ของผมที่เราจะฉีกกรอบการวัดผลแบบเดิมๆ แล้วหันมาโฟกัสสิ่งที่สำคัญที่สุดในโลกธุรกิจ นั่นก็คือ “กำไร” ครับ
ก่อนอื่นเราต้องเข้าใจว่า โมเดลที่ดีที่สุด ไม่ได้มีสูตรสำเร็จเดียว เพราะมันขึ้นอยู่กับ “ปัญหา” ที่เรากำลังแก้ ลองนึกภาพตามนะครับ…
- ถ้าเราสร้างโมเดลทำนายโรคระบาด 🦠: ความผิดพลาดที่น่ากลัวที่สุดคือการ “ตรวจไม่เจอคนป่วย” (False Negative) เพราะเขาอาจจะนำเชื้อไปแพร่ต่อได้ ในเคสนี้ เราจึงอยากได้โมเดลที่มี Sensitivity สูงมากๆ ยอมตรวจเจอคนที่ไม่ป่วยเกินมาบ้าง (False Positive) ดีกว่าปล่อยให้ผู้ป่วยหลุดรอดไปแม้แต่คนเดียว
- แต่ถ้าเราสร้างโมเดลอนุมัติสินเชื่อ 🏦: หายนะที่แท้จริงคือการ “อนุมัติสินเชื่อให้คนที่จะเบี้ยวหนี้” (False Positive) เพราะนั่นคือการขาดทุนโดยตรง ในเคสนี้ เราจึงต้องการโมเดลที่มี Specificity สูงลิ่ว เป็นเหมือนคนที่เชี่ยวชาญการ “ปฏิเสธ” ความเสี่ยงได้แม่นยำสุดๆ แม้จะต้องแลกกับการปฏิเสธลูกค้าดีๆ ไปบ้างก็ตาม
Project นี้คือเรื่องราวของสถานการณ์แบบที่สองครับ เราจะมาดูกันว่าการเปลี่ยนมุมมองจากการวัดผลด้วย Metric สวยๆ ไปสู่การวัดผลด้วย “ต้นทุนและความเสี่ยง” จะช่วยให้เราหาจุดสมดุลที่ทำกำไรสูงสุดเจอได้อย่างไร พร้อมแล้วก็ไปลุยกันเลย!
- บทนำ
- เครื่องมือวัดผล: เมื่อการ “ทายผิด” มีราคาไม่เท่ากัน
- ศึกคัดเลือกโมเดล: Accuracy สูง vs ความเสี่ยงต่ำ
- เลือกแล้วยังไม่จบ: สร้างเครื่องมือเพื่อ ‘ตีราคา’ ความผิดพลาดของโมเดล
- ปรับจูน Threshold เพื่อหาผลตอบแทนสูงสุด
- ส่องวิธีคิดของโมเดล
- บทสรุป: Key findings ที่ได้เรียนรู้จาก project นี้
เครื่องมือวัดผล: เมื่อการ “ทายผิด” มีราคาไม่เท่ากัน
ก่อนจะไปดูโมเดล ขอปูพื้นฐานเรื่องการวัดผลกันนิดนึงนะครับ ปกติเราจะใช้สิ่งที่เรียกว่า Confusion Matrix หรือตารางวัดความสับสนของโมเดล (โมเดลหรือเราสับสน 😂)
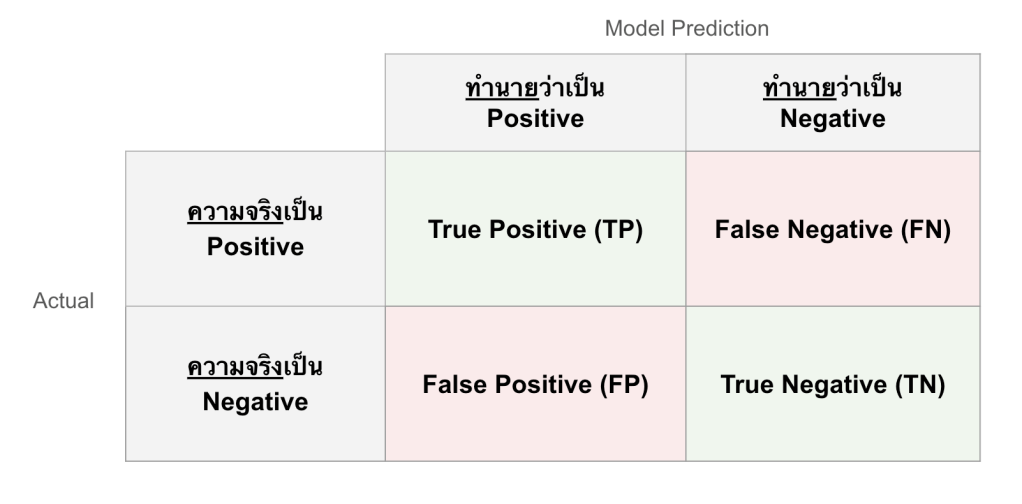
ง่ายๆ ก็คือ ตาราง 2×2 ที่บอกว่าโมเดลของเราทำงานได้ดีแค่ไหน:
- TP (True Positive): อนุมัติถูกคน → โมเดลทายว่า ‘สินเชื่อดี’ และเขาก็เป็นคนดีจริงๆ
- TN (True Negative): ปฏิเสธถูกคน → โมเดลทายว่า ‘สินเชื่อเสีย’ และเขาก็จะเบี้ยวหนี้จริงๆ
- FP (False Positive): อนุมัติผิดคน → โมเดลทายว่า ‘สินเชื่อดี’ แต่ดันเป็นสินเชื่อเสีย! (นี่แหละ หายนะ ของจริง💀)
- FN (False Negative): ปฏิเสธผิดคน → โมเดลทายว่า ‘สินเชื่อเสีย’ แต่จริงๆ เขาเป็นลูกค้าชั้นดี (เสียหายเป็นต้นทุนค่าเสียโอกาส หรือ Opportunity cost ซึ่งไม่เท่าเคสบน)
จากค่าทั้ง 4 นี้ เราสามารถนำมาคำนวณ metrics ได้ดังนี้:
- Accuracy (ความแม่นยำ): คือสัดส่วนที่โมเดลทายถูกโดยรวม (TP+TN) / ทั้งหมด เป็นการบอกภาพรวมกว้างๆ แต่ก็อาจทำให้เข้าใจผิดได้ถ้าข้อมูลไม่สมดุล (Imbalanced Data)
- Sensitivity (หรือ Recall): คือความสามารถของโมเดลในการ “ค้นหา” สินเชื่อดี ได้อย่างครบถ้วน (TP / (TP+FN)) ถ้าค่านี้สูง หมายความว่าเราไม่ค่อยพลาดลูกค้าดีๆ ไป
- Specificity: คือความสามารถของโมเดลในการ “คัดกรอง” สินเชื่อเสีย ได้อย่างแม่นยำ (TN / (TN+FP)) ถ้าค่านี้สูง หมายความว่าเราสามารถป้องกันความเสี่ยงจากการอนุมัติสินเชื่อเสียได้ดีมาก (ซึ่งเป็นพระเอกของ project นี้)
- AUC (Area Under the ROC Curve): คือค่าที่ใช้วัดประสิทธิภาพโดยรวมของโมเดลในการ “แยกแยะ” ระหว่างกลุ่มสินเชื่อดีและสินเชื่อเสีย โดยมีค่าตั้งแต่ 0.5 (เดาสุ่ม) ถึง 1.0 (สมบูรณ์แบบ) แม้ AUC จะเป็นเมตริกที่ดีในการเปรียบเทียบโมเดลในภาพรวม แต่มัน ไม่ได้คำนึงถึง “ต้นทุน” ของความผิดพลาดแต่ละแบบ ซึ่งในโลกธุรกิจมีความสำคัญไม่เท่ากัน ดังตัวอย่างที่กล่าวไปในบทนำ
ยอดเยี่ยมเลยครับ! เป็นการเพิ่มที่สำคัญมาก ทำให้คนอ่านเห็นภาพรวมของโปรเจกต์มากขึ้นว่าข้อมูลที่เอามาเทรนโมเดลมีที่มาที่ไปอย่างไร
ศึกคัดเลือกโมเดล: Accuracy สูง vs ความเสี่ยงต่ำ
ก่อนที่เราจะเปิดศึกคัดเลือกโมเดลกัน ผมขอเล่าย้อนความไปนิดนึงว่าข้อมูลที่ใช้ใน project นี้ไม่ได้สวยหรูมาตั้งแต่แรกนะครับ 😅
ผมนำข้อมูลมาจาก LendingClub Public Dataset ซึ่งเป็นข้อมูลการปล่อยสินเชื่อจริงๆ ขนาดมหึมา ผมได้ทำการสุ่มตัวอย่าง (Sampling) และทำความสะอาดข้อมูล (Data Cleaning) ไม่ว่าจะเป็นการเลือกเฉพาะฟีเจอร์ที่เกิดขึ้นก่อนการอนุมัติ, จัดการกับ Missing Values, และสร้างตัวแปรเป้าหมาย (Target) ซึ่งเป็นผลลัพธ์ในการทำนาย ได้แก่ good loan (จ่ายครบ) และ bad_loan (เบี้ยวหนี้) นั่นเอง
สำหรับใครที่อยากดูขั้นตอนการเตรียมข้อมูลแบบเต็มๆ พร้อมโค้ด 01_data_cleaning.R สามารถเข้าไปดูได้ที่ ลิงค์ GitHub นี้ได้เลยนะครับ ในบทความนี้เราจะขอข้ามไปที่ส่วนของการสร้างโมเดลกันเลย
ในโปรเจกต์นี้ ผมลองสร้างโมเดลยอดฮิต 2 ตัวมาสู้กันคือ:
- Logistic Regression (GLM)
- XGBoost
ผมใช้ caret ในการเทรนโมเดลทั้งสองด้วย code นี้ครับ (มีการใช้ smote เพื่อช่วยแก้ปัญหา Imbalanced data ด้วย)
# --- R/03_model_training.R ---
# Logis Regression (GLM) model training
model_glm <- train_model("glm", train, sampling = "smote")
# XGBoost model training
xgb_grid <- expand.grid(
nrounds = 100, max_depth = 3, eta = 0.1, gamma = 0,
colsample_bytree = 0.8, min_child_weight = 1, subsample = 0.8
)
model_xgb <- train_model("xgbTree", train, sampling = "smote", tuneGrid = xgb_grid)และนี่คือผลลัพธ์ที่ได้ครับ
| Model | Accuracy | Sensitivity | Specificity | Precision | AUC |
| Logistic Regression | 0.6552 | 0.6514 | **0.6696 | *0.8807 | 0.7218 |
| XGBoost | *0.7935 | *0.9704 | 0.1310 | 0.8070 | 0.7187 |
ถ้ามองแค่เผินๆ เราอาจจะรีบเลือก XGBoost ไปแล้วใช่ไหมครับ? Accuracy 0.79 แถม Sensitivity 0.97 โหดขนาดนี้! แปลว่ามันหาลูกค้าดีๆ เจอแทบไม่พลาดเลย
แต่เดี๋ยวก่อน! หากไปดูที่ช่อง Specificity จะพบว่า
XGBoost มี Specificity แค่ 0.13 เท่านั้น! กล่าวคือ “มันแทบจะแยกสินเชื่อเสียออกไปไม่ได้เลย” และปล่อยผ่านลูกค้าที่น่าจะเบี้ยวตัง (ความเสี่ยง)เข้ามาเต็มๆ ซึ่งสวนทางกับเป้าหมายของเราอย่างสิ้นเชิง
ในทางกลับกัน Logistic Regression แม้ Accuracy จะน้อยกว่า แต่มี Specificity สูงถึง 0.67 หมายความว่ามันทำหน้าที่เป็น “ยามเฝ้าประตู” คัดกรองความเสี่ยงได้ดีกว่ามาก
ในโลกของสินเชื่อ การอนุมัติผิดคน (FP) หนึ่งครั้ง ได้รับความเสียหายมากกว่าการปฏิเสธลูกค้าดีๆ (FN) ไปหลายเท่า ดังนั้นสำหรับในเคส Loan Approval Model นี้ การเลือกโมเดล Logistic Regression จะเหมาะสมมากกว่าครับ อารมณ์ว่า “ปลอดภัยไว้ก่อนดีกว่านะเพื่อน”
เลือกแล้วยังไม่จบ: สร้างเครื่องมือเพื่อ ‘ตีราคา’ ความผิดพลาดของโมเดล
หลังจากเราเลือก Logistic Regression ที่เป็นเหมือน “ยามเฝ้าประตู” สุดเข้มงวดมาแล้ว หลายคนอาจจะคิดว่าจบแล้ว…แต่จริงๆ แล้ว เกมที่สนุกที่สุดเพิ่งจะเริ่มครับ
เพราะถึงเราจะได้โมเดลที่ใช่ แต่คำถามสำคัญคือ “เราจะใช้งานมันอย่างไรให้ฉลาดและได้ผลตอบแทนสูงที่สุด?”
โดยปกติแล้ว โมเดล Logistic Regression ไม่ได้ตอบเราแค่ “อนุมัติ” หรือ “ปฏิเสธ” ตรงๆ นะครับ แต่มันจะให้ “คะแนนความน่าจะเป็น” (Probability) กลับมา เช่น “เคสนี้มีโอกาสเป็นสินเชื่อดี 75%”
Threshold ก็คือ “เกณฑ์ตัดสินใจ” ที่เราตั้งขึ้นมาเองนี่แหละครับ โดย default โมเดลจะถูกตั้งไว้ที่ 0.5 (หรือ 50%) หมายความว่าถ้าคะแนนความน่าจะเป็นสูงกว่า 0.5 ก็อนุมัติ ต่ำกว่าก็ปฏิเสธ
แต่นี่คือจุดสำคัญครับ…ใครบอกว่า 0.5 คือเกณฑ์ที่ดีที่สุดสำหรับโจทย์ของเราล่ะ? ถ้าเราอยากจะเข้มงวดมากๆ เราอาจจะตั้งเกณฑ์ไว้ที่ 0.7 (ต้องมั่นใจ 70% ขึ้นไปถึงจะปล่อย) ก็ได้! การปรับหา “เกณฑ์” หรือ Threshold ที่เหมาะสมกับธุรกิจนี่แหละครับ คือการจูนโมเดลที่แท้จริง
ทุกคนยังจำเรื่องตอนต้นได้ไหมครับ ว่าความผิดพลาดแต่ละแบบมันสร้างความเสียหายไม่เท่ากัน? ตอนนี้แหละที่เราจะเอากฎข้อนั้นมาใช้จริง โดยการ “ตีราคา” ความผิดพลาดและความสำเร็จแต่ละแบบให้เป็นตัวเงิน!
ผมได้ตั้งสมมติฐานทางธุรกิจขึ้นมาว่า:
Total_Cost = Avg. Loan Amount * [(TP * 15%) - (FP * 85%) - (FN * 3%)]- อนุมัติถูกคน (TP): เราดีใจ ได้กำไรจากดอกเบี้ย +15% ของวงเงิน
- อนุมัติผิดคน (FP): เราเจ็บ ขาดทุนเงินต้นและค่าติดตามหนี้ -85% ของวงเงิน
- ปฏิเสธผิดคน (FN): เราเสียดาย เสียโอกาสทำกำไรไป -3% ของวงเงิน
Note: Avg. Loan Amount = 518,177 บาท (คำนวณจาก dataset)
จากนั้น เราจึงแปลง logic ทางธุรกิจนี้ให้กลายเป็นฟังก์ชัน calculate_cost ใน R เพื่อคำนวณกำไร/ขาดทุนสุทธิที่เกิดขึ้นจริงจากการตัดสินใจของโมเดล ดังนี้ครับ
# --- R/02_functions.R ---
calculate_cost <- function(pred_prob, actual, threshold) {
# Convert probability to class based on threshold
pred_class <- ifelse(pred_prob >= threshold, "good_loan", "bad_loan")
pred_class <- factor(pred_class, levels = c("good_loan", "bad_loan"))
actual <- factor(actual, levels = c("good_loan", "bad_loan"))
# Create confusion matrix
cm <- table(
Predicted = factor(pred_class, levels = c("good_loan", "bad_loan")),
Actual = factor(actual, levels = c("good_loan", "bad_loan"))
)
TP <- cm["good_loan", "good_loan"]
FP <- cm["good_loan", "bad_loan"]
FN <- cm["bad_loan", "good_loan"]
TN <- cm["bad_loan", "bad_loan"]
usd_to_thb <- 36.5 # Exchange rate
# Calculate average profit/loss per case in THB
profit_per_tp <- loan_data %>%
filter(loan_status == "good_loan") %>%
summarise(val = mean(loan_amnt * 0.15)) %>%
pull(val) * usd_to_thb
loss_per_fp <- loan_data %>%
filter(loan_status == "bad_loan") %>%
summarise(val = mean(loan_amnt * 0.85)) %>%
pull(val) * usd_to_thb
loss_per_fn <- loan_data %>%
filter(loan_status == "good_loan") %>%
summarise(val = mean(loan_amnt * 0.03)) %>%
pull(val) * usd_to_thb
# Calculate total net profit/loss
total_cost <- (TP * profit_per_tp +
FP * -loss_per_fp +
FN * -loss_per_fn) / 1e6 # Convert to millions THB
return(data.frame(
Threshold = threshold,
TP = TP, FP = FP, FN = FN, TN = TN,
Specificity = round(TN / (TN + FP), 4),
Sensitivity = round(TP / (TP + FN), 4),
Total_Cost = round(total_cost, 4)
))
}
เท่ากับตอนนี้เรามี “เครื่องวัดมูลค่า” ที่จะบอกได้แล้วว่าการตัดสินใจของโมเดลที่แต่ละระดับความมั่นใจนั้น “สร้างเงิน” หรือ “เผาเงิน” กันแน่!
ทำให้ในลำดับถัดไป เราสามารถหา “จุดที่ได้ผลตอบแทนสูงสุด” ได้แล้วครับ!
ปรับจูน Threshold เพื่อหาผลตอบแทนสูงสุด
เป้าหมายของเราตอนนี้คือการหา “เกณฑ์ตัดสินใจ” หรือ Threshold ที่ดีที่สุด ที่จะทำให้เราได้ผลตอบแทนสูงสุด เราจะทำการทดลองโดยการไล่เปลี่ยนค่า Threshold ไปเรื่อยๆ ตั้งแต่เข้มงวดน้อย (0.30) ไปจนถึงเข้มงวดมาก (0.90) แล้วให้ฟังก์ชัน calculate_cost ของเราคำนวณผลกำไรสุทธิออกมา ดัง code นี้ครับ
# --- R/04_threshold_tuning.R ---
# Predict probabilities on the test set
glm_probs <- predict(model_glm, newdata = test, type = "prob")[, "good_loan"]
# Create a sequence of thresholds to test
thresholds <- seq(0.3, 0.9, by = 0.05)
# Loop through each threshold and calculate the business cost/profit
cost_results <- map_df(thresholds, function(thresh) {
calculate_cost(glm_probs, test$loan_status, thresh)
})และผลลัพธ์ที่ได้…ก็คือตารางนี้ครับ!
| Threshold | TP | FP | FN | TN | Sensitivity | Specificity | Total Profit (Million THB) |
|---|---|---|---|---|---|---|---|
| 0.30 | 24426 | 4954 | 2596 | 2261 | 0.9039 | 0.3134 | -540.96 |
| 0.35 | 23084 | 4299 | 3938 | 2916 | 0.8543 | 0.4042 | -348.61 |
| 0.40 | 21545 | 3660 | 5477 | 3555 | 0.7973 | 0.4927 | -182.45 |
| 0.45 | 19687 | 3020 | 7335 | 4195 | 0.7286 | 0.5814 | -45.64 |
| 0.50 | 17602 | 2384 | 9420 | 4831 | 0.6514 | 0.6696 | +68.01 |
| 0.60 | 12999 | 1335 | 14023 | 5880 | 0.4811 | 0.8150 | +146.60 |
| 0.65 | 10613 | 944 | 16409 | 6271 | 0.3928 | 0.8692 | +113.22 |
| 0.70 | 8324 | 607 | 18698 | 6608 | 0.3080 | 0.9159 | +62.70 |
| 0.75 | 6155 | 379 | 20867 | 6836 | 0.2278 | 0.9475 | -29.49 |
| 0.80 | 4211 | 201 | 22811 | 7014 | 0.1558 | 0.9721 | -124.90 |
จะสังเกตได้ว่า Threshold 0.50 (ค่า Default) เราได้กำไร 68 ล้านบาท แต่พอเราเข้มงวดขึ้น ขยับเกณฑ์ไปที่ 0.60 กำไรพุ่งไปถึง 146.60 ล้านบาท! 🚀
เพื่อให้เห็นภาพชัดๆ ลองดูกราฟนี้ครับ

นี่แหละครับคือจุดที่ใช่ จุดที่ได้ผลตอบแทนสูงสุด การตัดสินใจของเราไม่ได้อิงจากความรู้สึก แต่มาจากข้อมูลที่พิสูจน์ได้ว่าการตั้งเกณฑ์ที่ 0.60 คือกลยุทธ์ที่ฉลาดและสร้างผลตอบแทนให้ธุรกิจได้ดีที่สุดครับ
ส่องวิธีคิดของโมเดล
คำถามคลาสสิกของชาว Data Science คือ ระหว่างโมเดล ‘กล่องดำ’ (Black Box) ที่แม่นยำสุดๆ กับ ‘กล่องแก้ว’ (Glass Box) ที่โปร่งใส เราควรเลือกอะไรดี?
คำตอบคือแล้วแต่ความต้องการครับ บางธุรกิจขอแค่ผลลัพธ์แม่นๆ ก็แฮปปี้แล้ว ไม่ได้สนใจว่าหลักการเป็นยังไง แต่หลายๆ ธุรกิจ ก็อยากได้ความโปร่งใสที่สามารถตรวจสอบและอธิบายได้ว่าทำไมโมเดลจึงเลือกทำนายแบบนี้
โมเดลประเภท ‘Glass Box’ ที่นิยมกันก็คือโมเดลสายสถิติอย่าง Logistic Regression (ที่เราเลือกมา) หรือ Decision Trees เพราะเราสามารถดูเหตุผลเบื้องหลังการตัดสินใจของมันได้ง่าย
ในบทนี้ เราจะมาเปิดกล่องแก้วของโมเดลเรากัน โดยใช้ 2 เครื่องมือหลักๆ คือ
- ภาพรวม (Overall): ดูว่าโดยรวมแล้วโมเดลให้ความสำคัญกับปัจจัยไหนบ้าง (Feature Importance)
- รายเคส (Case-by-Case): เจาะลึกเป็นรายคนเลยว่าทำไมเคสนี้ถึงถูกปฏิเสธ ด้วยเทคนิคที่เรียกว่า LIME
ปัจจัยภาพรวม (Overall) ที่โมเดลของเราใช้ตัดสินใจ
ก่อนอื่น เรามาดูกันว่าปัจจัยอะไรที่ โมเดล Logistic Regression ของเราให้ความสำคัญมากที่สุดในการตัดสินใจ โดยเราจะใช้ฟังก์ชัน varImp() จากแพ็คเกจ caret มาช่วยจัดอันดับความสำคัญของตัวแปร
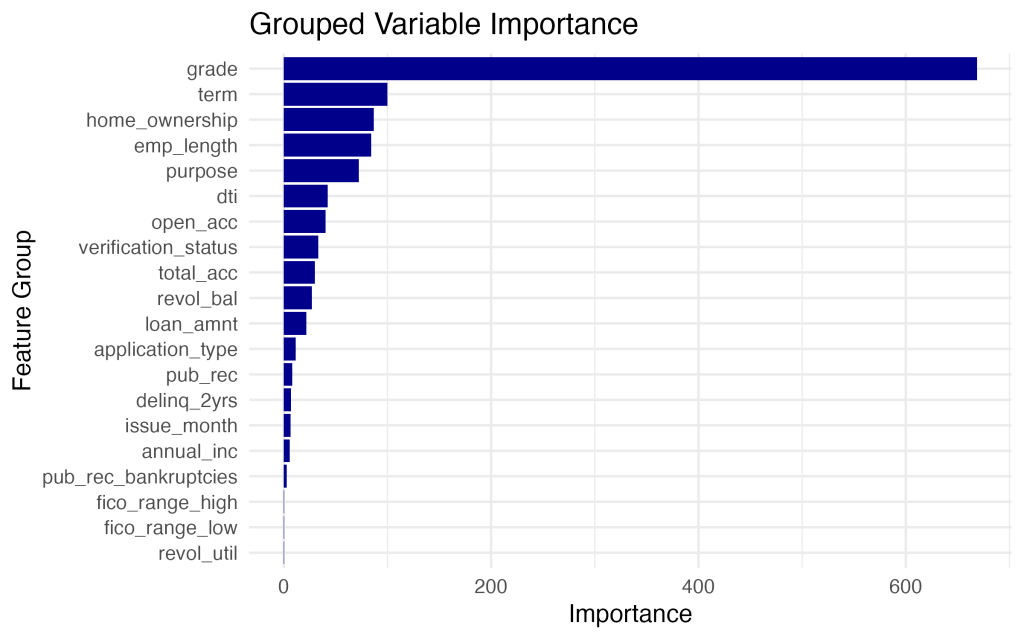
จากกราฟจะเห็นชัดเลยว่า Grade (เกรดสินเชื่อ), Term (ระยะเวลาผ่อน), และ Home Ownership (การถือครองที่อยู่อาศัย) คือ 3 ปัจจัยที่มีอิทธิพลสูงสุด
เจาะลึกรายบุคคล: ทำไมเคสนี้ถึงอนุมัติหรือโดนปฏิเสธ?
หากเราอยากตอบคำถามให้ได้ว่า “ทำไมผู้สมัคร A ถึงถูกปฏิเสธ ทั้งที่โปรไฟล์ก็ดูดี?”
เพื่อตอบคำถามนี้ เราจะใช้เทคนิคที่ชื่อว่า LIME (Local Interpretable Model-agnostic Explanations) มาช่วย “แปล” ความคิดของโมเดลในการตัดสินใจเคสต่อเคสครับ
ผมลองหยิบเคสที่คะแนนก้ำกึ่ง (เกือบจะผ่าน) มาหนึ่งเคส แล้วใช้ LIME วิเคราะห์ด้วย code แบบนี้ครับ
# --- R/06_lime_explainer.R ---
# Select a borderline case for explanation
borderline_data <- test[borderline_idx, , drop = FALSE]
# Create an explainer object
explainer <- lime(train, model = model_glm, bin_continuous = TRUE)
# Explain the prediction for this single case
explanation <- explain(
x = borderline_data,
explainer = explainer,
n_features = 10,
labels = "bad_loan" # Explain why it was predicted as bad_loan
)และนี่คือ chart ที่เราได้จาก code นี้ครับ:
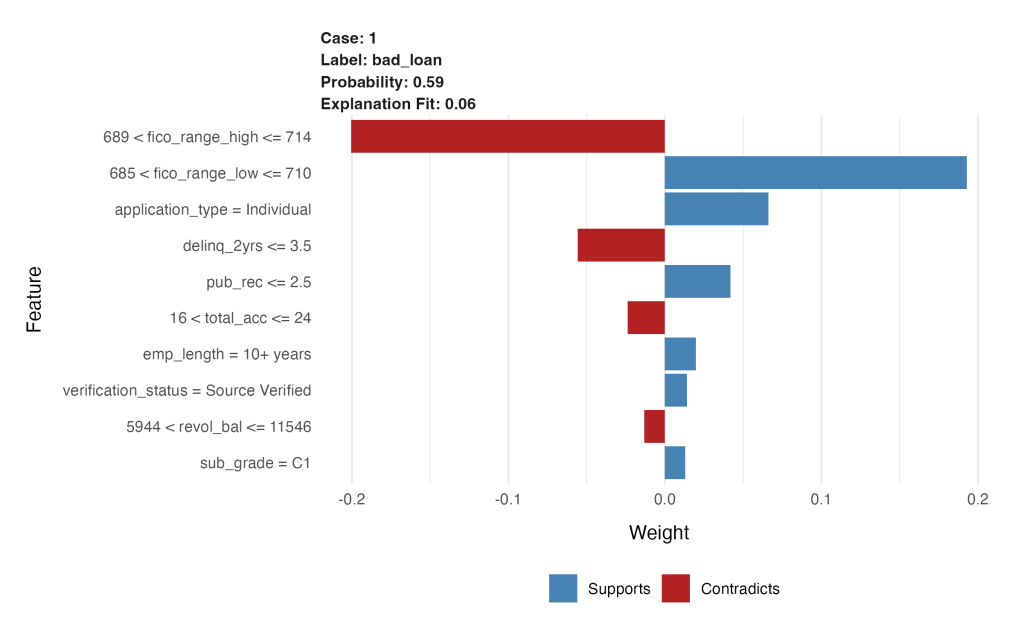
- สีน้ำเงิน (Supports): คือปัจจัยที่ “สนับสนุน” หรือ “ส่งเสริม” ให้โมเดลทำนายว่าเคสนี้เป็น
bad_loan - สีแดง (Contradicts): คือปัจจัยที่ “คัดค้าน” การทำนายว่าเป็น
bad_loan(หรืออีกนัยหนึ่งคือ เป็นปัจจัยที่ทำให้โมเดลคิดว่าเคสนี้อาจจะเป็นgood_loan)
| Feature | Value / Bin | Contribution to Prediction (bad_loan) |
|---|---|---|
fico_range_high (689–714) | Moderate credit score | Strongly contradicts ‘bad_loan’ |
fico_range_low (685–710) | Moderate credit score | Strongly supports ‘bad_loan’ |
application_type = Individual | Single applicant | Supports ‘bad_loan’ |
delinq_2yrs ≤ 3.5 | Few delinquencies | Contradicts ‘bad_loan’ |
pub_rec ≤ 2.5 | Low public record count | Supports ‘bad_loan’ |
total_acc = 16–24 | Moderate account count | Contradicts ‘bad_loan’ |
emp_length = 10+ years | Long employment | Supports ‘bad_loan’ |
revol_bal = 5,944–11,546 | Medium revolving balance | Slightly contradicts ‘bad_loan’ |
verification_status = Verified | Income source verified | Slightly supports ‘bad_loan’ |
sub_grade = C1 | Mid-tier sub-grade | Slightly contradicts ‘bad_loan’ |
LIME ช่วยเผยให้เห็น “สัญชาตญาณ” หรือรูปแบบที่ซับซ้อนที่โมเดลได้เรียนรู้มาจากข้อมูลจำนวนมหาศาล ซึ่งบางครั้งก็เป็นเหตุผลที่สวนทางกับความรู้สึกของเรา
ลองนึกภาพว่าโมเดลของเราเป็นเหมือน ผู้จัดการสินเชื่อที่มีประสบการณ์สูงมาก นะครับ
เมื่อเจอผู้สมัครคนหนึ่งที่โปรไฟล์ดูก้ำกึ่ง ผู้จัดการคนนี้ก็เริ่มวิเคราะห์ เขาเห็นว่า “เอ…ผู้สมัครคนนี้ประวัติการจ่ายหนี้ก็ดีนี่นา” ซึ่งเป็นข้อดีที่ชัดเจน แต่ด้วยประสบการณ์ที่ผ่านมา เขากลับสังเกตเห็นบางอย่างที่น่ากังวล เขาอาจจะเคยเจอคนที่มีโปรไฟล์แบบนี้เป๊ะๆ (เช่น มีคะแนนเครดิตอยู่ในช่วงนี้พอดี) แล้วสุดท้ายมักจะมีปัญหาทางการเงินในภายหลัง
สุดท้าย เขานี้จึงตัดสินใจที่จะ “ปฏิเสธ” ไปก่อนเพื่อความปลอดภัย โดยให้น้ำหนักกับ “รูปแบบความเสี่ยงที่เคยเจอในอดีต” มากกว่า “คุณสมบัติที่ดูดีผิวเผิน” ครับ
บทสรุป: Key findings ที่ได้เรียนรู้จาก project นี้
” Every prediction is a financial bet. We optimized for expected monetary gain, not just model score.”
- Business Understanding is crucial: การเปลี่ยนความผิดพลาด (Misclassifications) ให้เป็น ‘ต้นทุน’ ทางการเงิน ทำให้เราสามารถ ปรับจูนโมเดลเพื่อหา ‘ผลตอบแทน’ สูงสุดได้จริง ซึ่งเป็นเป้าหมายที่เหนือกว่าการจูนโมเดลทั่วไป
- Model interpretability matters: การเลือกใช้โมเดลขึ้นอยู่กับความต้องการทางธุรกิจ บางกรณีอาจให้ความสำคัญกับ ความแม่นยำ (Accuracy) สูงสุดเพียงอย่างเดียว ในขณะที่หลายธุรกิจต้องการ ความโปร่งใส (Transparency) เพื่อให้สามารถตรวจสอบและอธิบายเหตุผลเบื้องหลังการทำนายได้
- สมดุลที่ใช่ระหว่าง Sensitivity vs Specificity: การให้น้ำหนักกับ Metric ไหนมากกว่ากันนั้นขึ้นอยู่กับโจทย์ของธุรกิจโดยตรง โมเดลที่ Sensitivity สูงลิ่วอย่าง XGBoost อาจหาลูกค้าเจอเยอะจริง แต่ก็อนุมัติ “ความเสี่ยง” เข้ามาด้วย การเลือก Logistic Regression ที่มี Specificity สูงกว่าจึงเป็นการสร้างสมดุลที่ดีกว่าสำหรับธุรกิจสินเชื่อ
- Business Alignment: แนวทางนี้ไม่เพียงแต่สร้างโมเดลที่ดีในทางเทคนิค แต่ยังตอบโจทย์ตัวชี้วัด (KPIs) ของฝ่ายการเงิน และฝ่ายบริหารความเสี่ยงโดยตรง เพราะมันสามารถตอบคำถามได้รูปแบบของ ‘กำไร-ขาดทุน’ (P&L)
ขอบคุณทุกคนที่ติดตามอ่านมาจนจบนะครับ! สำหรับใครที่อยากดูโค้ดการทำงานทั้งหมด สามารถเข้าไปดูได้ที่ ลิงค์ GitHub และหากมีคำถามหรืออยากแลกเปลี่ยนไอเดีย สามารถติดต่อเข้ามาได้เลยนะครับ 😊🤍
