Tag: data

บทนำ

เคยไหมครับ… เวลาอยู่ในห้องประชุมเพื่อตัดสินใจเรื่องสำคัญทางการตลาด

“ผมว่าปุ่มสีเขียวเด่นกว่านะ”

“แต่พี่รู้สึกว่าสีแดงกระตุ้นการคลิกได้ดีกว่า”

“หรือจะลองใช้ข้อความโฆษณาแบบ A ดี?”

“ไม่ๆ ผมว่าแบบ B โดนใจวัยรุ่นกว่าเยอะ”

การถกเถียงเหล่านี้มักจบลงด้วยการตัดสินใจที่อิงจาก “Gut Feeling”—ความรู้สึกส่วนตัว หรือ ประสบการณ์ที่ผ่านมา ซึ่งไม่ใช่เรื่องผิด แต่ก็ไม่ใช่หนทางที่ดีที่สุดเสมอไป

ในยุคที่ทุกการกระทำของลูกค้ามี “ข้อมูล” ทิ้งไว้เป็นร่องรอยเอาไว้ เรามีเครื่องมือที่ทรงพลังกว่าการคาดเดา นั่นคือการเปลี่ยนบทสนทนาจาก “ผมรู้สึกว่า…” ไปเป็น “ข้อมูลพิสูจน์ว่า…” ผ่านกระบวนการที่เรียกว่า A/B Testing

A/B Testing (หรือที่เรียกว่า Split Testing) คือกระบวนการทดลองเชิงเปรียบเทียบ เพื่อหาคำตอบอย่างเป็นระบบว่า ระหว่างองค์ประกอบ 2 version (หรือมากกว่า) version ไหนทำงานได้ดีกว่ากันตามเป้าหมายที่เราตั้งไว้

หัวใจของมันคือการแบ่งผู้ใช้งาน (users) ออกเป็นกลุ่มๆ แบบสุ่ม และแต่ละกลุ่มจะได้รับประสบการณ์ที่แตกต่างกันไป:

• กลุ่ม A (Control): คือ version “ควบคุม” ซึ่งมักจะเป็น version ที่ใช้งานอยู่ในปัจจุบัน หรือเป็น version พื้นฐานที่เราใช้เป็นเกณฑ์เปรียบเทียบ
• กลุ่ม B (Variant): คือ version “ท้าชิง” ที่เราสร้างขึ้นโดยมีสมมติฐานว่าจะทำงานได้ดีกว่า

หลังจากปล่อยให้ผู้ใช้ทั้งสองกลุ่ม ได้ลองใช้ version ของตัวเองไประยะหนึ่ง เราจะเก็บข้อมูลและวัดผลจากแต่ละกลุ่มด้วย ตัวชี้วัด (Metric) เดียวกัน เช่น อัตราการคลิก (Click-through Rate) หรือ อัตราการมีส่วนร่วม (Engagement Rate) เป็นต้น

สุดท้าย เราจะนำผลลัพธ์ที่ได้มาวิเคราะห์ด้วยเครื่องมือทางสถิติ เพื่อตัดสินว่าความแตกต่างที่เกิดขึ้นนั้น มีนัยสำคัญทางสถิติ (Statistically Significant) หรือไม่ หรือเป็นแค่เรื่องบังเอิญ

สำหรับ project นี้ ผมใช้ข้อมูล A/B Testing Data for a Conservation Campaign จาก Kaggle และใช้ Jupyter Notebook ในการเขียน Python ซึ่งทุกคนสามารถทำตามได้เลยครับ

โดยตัว dataset จะประกอบไปด้วย:

• user id: User ID (unique)
• message_type: ประเภทของข้อความที่ส่งหาผู้ใช้ (‘Personalized’ หรือ ‘Generic’)
• engaged: ผู้ใช้มีส่วนร่วมหรือไม่ (True/False)
• total_messages_seen: จำนวนข้อความที่ผู้ใช้เห็น
• most_engagement_day: วันที่ผู้ใช้มีส่วนร่วมมากที่สุด
• most_engagement_hour: ชั่วโมงที่ผู้ใช้มีส่วนร่วมมากที่สุด

โดยจุดประสงค์ คือการตอบคำถามให้ได้ว่า การส่งข้อความแบบ Personalized ช่วยเพิ่มการมีส่วนร่วม (Engagement) ของผู้ใช้ได้จริงหรือไม่ และผลลัพธ์ที่ได้นั้นมีนัยสำคัญทางสถิติพอที่จะนำไปใช้ตัดสินใจทางธุรกิจได้หรือไม่ โดยมีขั้นตอนการวิเคราะห์ 4 ขั้นตอนหลักดังนี้:

1. เตรียมข้อมูล (Data Processing): เราจะใช้ PySpark เพื่อทำความสะอาดข้อมูลขนาดใหญ่ (580,000+ แถว) ให้พร้อมสำหรับการวิเคราะห์
2. ออกแบบการทดลอง (Experiment Design): เราจะกำหนดเป้าหมายทางธุรกิจ (Minimum Detectable Effect หรือ MDE) และใช้ Power Analysis เพื่อคำนวณหาขนาดกลุ่มตัวอย่าง (Sample Size) ที่เล็กที่สุดที่จำเป็นสำหรับการทดลอง
3. วิเคราะห์เชิงสถิติ (Statistical Analysis): เราจะใช้ Two-Proportion Z-test และ Confidence Intervals เพื่อพิสูจน์ว่าความแตกต่างของ Engagement Rate ที่เราเห็นนั้นเป็นของจริง หรือเป็นแค่เรื่องบังเอิญ
4. สรุปผลเชิงธุรกิจ (Business Conclusion): สุดท้าย เราจะแปลผลตัวเลขทางสถิติทั้งหมด ให้กลายเป็นข้อเสนอแนะที่จับต้องได้เพื่อนำไปใช้งานจริง

ขั้นตอนที่ 1: เตรียมข้อมูล (Data Processing) ด้วย PySpark

เมื่อต้องจัดการกับข้อมูลขนาดใหญ่ (580,000+ แถว) เครื่องมืออย่าง Excel หรือ pandas อาจทำงานได้ช้าหรือไม่เพียงพอ เราจึงเลือกใช้ PySpark ซึ่งเป็นเครื่องมือที่ออกแบบมาเพื่อประมวลผลข้อมูลขนาดใหญ่โดยเฉพาะครับ

PySpark คืออะไร?

PySpark คือ Python API สำหรับ Apache Spark ซึ่งเป็นเครื่องมือประมวลผลข้อมูลขนาดใหญ่แบบ Distributed Computing

ถ้าเพื่อนๆ เคยใช้ pandas ซึ่งเป็น library ยอดนิยมในการจัดการข้อมูลใน Python จะพบว่าหน้าตา code ของ PySpark นั้นคล้ายกันมาก มีคำสั่งอย่าง .select(), .filter(), .groupBy() ที่ทำให้เรียนรู้ได้ไม่ยาก

แต่ความแตกต่างสำคัญอยู่ที่ “เบื้องหลังการทำงาน”:

• pandas: ทำงานบนคอมพิวเตอร์เดียว (Single Machine) ใช้ทรัพยากร (CPU, RAM) แค่ในเครื่องนั้นเครื่องเดียว
• PySpark: ถูกออกแบบมาให้ “กระจายงาน” ไปทำพร้อมๆ กันบนคอมพิวเตอร์หลายๆ เครื่อง (เรียกว่า Cluster) ทำให้สามารถจัดการข้อมูลที่ใหญ่เกินกว่าที่คอมพิวเตอร์เครื่องเดียวจะรับไหวได้

จริงๆ แล้วข้อมูลจำนวนประมาณ 580,000 แถวใน project นี้ pandas ยังรับมือไหวครับ แต่หากวันหนึ่งข้อมูลของเราเติบโตจากหลักแสนเป็นหลักสิบล้าน หรือร้อยล้านแถว การใช้ pandas จะทำงานไม่ได้หรือไม่ก็ช้ามากจนใช้งานจริงไม่ได้ แต่ PySpark ที่เราเขียนไว้นี้ จะยังคงทำงานได้ดีเหมือนเดิม เป็นการสร้าง Pipeline ที่รองรับการขยายตัวในอนาคต (Scalable) ครับ

1.1 Setup and Data Loading

ในส่วนแรกนี้ เราจะเริ่มต้นด้วยการสร้าง “ประตู” เชื่อมต่อไปยัง Spark ที่เรียกว่า SparkSession ซึ่งเป็นจุดเริ่มต้นของการทำงานทั้งหมดกับ Spark ครับ จากนั้นเราจะกำหนด Schema หรือพิมพ์เขียวของข้อมูล เพื่อบอกให้ Spark ทราบล่วงหน้าว่าข้อมูลในแต่ละคอลัมน์เป็นประเภทใด (เช่น ตัวเลข, ข้อความ) การทำเช่นนี้ช่วยป้องกันข้อผิดพลาดและทำให้ Spark อ่านข้อมูลได้เร็วยิ่งขึ้น สุดท้าย เราจึงสั่งให้ Spark อ่านไฟล์ .csv โดยใช้ Schema ที่เรากำหนด

หมายเหตุ: code นี้ถูกรันบน Google Colab หากต้องการทำตามในนี้เหมือนกัน ให้ run คำสั่ง !pip install pyspark เพื่อติดตั้ง library และใช้ from google.colab import files เพื่ออัปโหลดไฟล์ conservation_dataset.csv ก่อนนะครับ

from pyspark.sql import SparkSession
from pyspark.sql.types import StructType, StructField, StringType, BooleanType, IntegerType

# 1. Initialize Spark Session
spark = SparkSession.builder \
    .appName("Engagement_AB_Test_Processing") \
    .getOrCreate()

# 2. Define the full data schema
schema = StructType([
    StructField("row_index", IntegerType(), True),
    StructField("user_id", StringType(), True),
    StructField("message_type", StringType(), True),
    StructField("engaged", BooleanType(), True),
    StructField("total_messages_seen", IntegerType(), True),
    StructField("most_engagement_weekday", StringType(), True),
    StructField("most_engagement_hour", IntegerType(), True)
])

# 3. Load data from CSV with the defined schema
df = spark.read.csv("conservation_dataset.csv", header=True, schema=schema)

1.2 Data Cleaning

นี่คือขั้นตอนที่สำคัญที่สุดเพื่อให้ผลการทดลองน่าเชื่อถือ เพราะข้อมูลที่ “สกปรก” จะนำไปสู่ข้อสรุปที่ผิดพลาดได้เสมอ (Garbage In, Garbage Out) ซึ่งประกอบด้วย 3 การตรวจสอบหลัก:

1. na.drop: เราจะลบแถวใดๆ ก็ตามที่ไม่มีข้อมูลในคอลัมน์ user_id หรือ message_type เพราะข้อมูลเหล่านั้นไม่สามารถบอกเราได้ว่าเป็นของผู้ใช้คนไหน หรืออยู่กลุ่มทดลองใด จึงไม่เป็นประโยชน์ต่อการวิเคราะห์ A/B Test
2. groupBy/filter: เราตรวจสอบความถูกต้องของการทดลองโดยการเช็คว่ามีผู้ใช้คนใดอยู่ในทั้ง 2 กลุ่ม (Personalized และ Generic) หรือไม่ ซึ่งเป็นสถานการณ์ที่ต้องไม่เกิดขึ้นใน A/B Test ที่ดี code ส่วนนี้จะนับจำนวนกลุ่มที่แต่ละ user_id สังกัดอยู่ ถ้ามีค่ามากกว่า 1 จะต้องถูกคัดออก
3. dropDuplicates: เพื่อให้แน่ใจว่าผู้ใช้ 1 คนจะถูกนับเพียง 1 ครั้งในแต่ละกลุ่ม เราจึงลบแถวที่ซ้ำซ้อนกันของคู่ user_id และ message_type ออกไป

from pyspark.sql.functions import col, countDistinct

# 1. Drop rows with nulls in key columns ('user_id', 'message_type')
df_clean = df.na.drop(subset=["user_id", "message_type"])

# 2. Check for users assigned to multiple groups
users_in_multiple_groups = df_clean.groupBy("user_id") \
    .agg(countDistinct("message_type").alias("group_count")) \
    .filter(col("group_count") > 1)

if users_in_multiple_groups.count() > 0:
    print(f"Found {users_in_multiple_groups.count()} users in multiple groups. Removing them.")
    user_ids_to_remove = users_in_multiple_groups.select("user_id")
    df_clean = df_clean.join(user_ids_to_remove, on="user_id", how="left_anti")
else:
    print("No users found in multiple groups. Data is clean.")

# 3. Handle duplicates: If a user has multiple rows in the same group, keep only the first one
df_clean = df_clean.dropDuplicates(["user_id", "message_type"])

1.3 Transformation & Aggregation

หลังจากข้อมูลสะอาดแล้ว ขั้นตอนสุดท้ายคือการแปลงข้อมูลและสรุปผลให้อยู่ในรูปแบบที่พร้อมนำไปวิเคราะห์ทางสถิติต่อไป

• Transformation: ในการคำนวณ Engagement Rate เราจำเป็นต้องใช้ตัวเลข เราจึงสร้างคอลัมน์ใหม่ชื่อ engaged_numeric โดยแปลงค่า True เป็น 1 และ False เป็น 0 เพื่อให้สามารถนำไปบวกลบหาผลรวมได้
• Aggregation: เราจะจัดกลุ่มข้อมูลทั้งหมดตาม message_type จากนั้นในแต่ละกลุ่ม (Personalized และ Generic) ให้ทำการสรุปผล 3 อย่างคือ: 1) นับจำนวนผู้ใช้ทั้งหมด (n_users), 2) หาผลรวมของคนที่ engaged (n_engaged), และ 3) นำสองค่ามาหารกันเพื่อหา engagement_rate

from pyspark.sql.functions import when, count, sum as _sum

# Transform 'engaged' (boolean) to 'engaged_numeric' (0 or 1)
df_transformed = df_clean.withColumn("engaged_numeric", when(col("engaged") == True, 1).otherwise(0))

# Aggregate data by message_type to get the final summary
summary = df_transformed.groupBy("message_type").agg(
    count("user_id").alias("n_users"),
    _sum("engaged_numeric").alias("n_engaged"),
    (_sum("engaged_numeric") / count("user_id")).alias("engagement_rate")
)

# Show the final summary table
summary.show()

Output:

+------------+-------+---------+--------------------+
|message_type|n_users|n_engaged|   engagement_rate  |
+------------+-------+---------+--------------------+
|Personalized| 564577|    14423|0.025546559636683747|
|     Generic|  23524|      420| 0.01785410644448223|
+------------+-------+---------+--------------------+

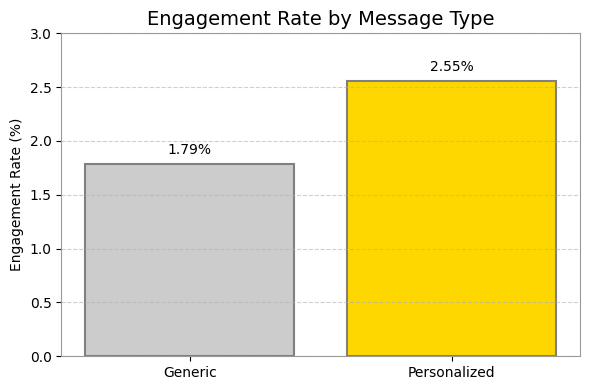
จะสังเกตได้ว่า กลุ่ม Personalized มี Engagement Rate สูงกว่าอยู่ +0.77% ซึ่งความแตกต่างนี้เป็นของจริงหรือเป็นแค่เรื่องบังเอิญ? เราจะยังสรุปไม่ได้ จนกว่าจะได้พิสูจน์ทางสถิติครับ

1.4 Exporting the Summary Data

หลังจากที่เราได้ตารางสรุปผล (summary) ซึ่งมีขนาดเล็กแล้ว ขั้นตอนสุดท้ายคือการบันทึกตารางนี้ลงในไฟล์ .csv เพื่อนำไปใช้ต่อในขั้นตอนที่ 3 ครับ การทำเช่นนี้เป็นวิธีปฏิบัติทั่วไป เพื่อที่เราจะสามารถปิด Spark Session ที่ใช้ทรัพยากรสูง และเปลี่ยนไปทำงานต่อในสภาพแวดล้อมที่เบากว่าได้

# Note: This part is specific to Google Colab for saving to Google Drive.
from google.colab import drive
drive.mount('/content/drive')

# 1. Convert Spark DataFrame to a Pandas DataFrame for easy CSV saving.
summary_pd = summary.toPandas()

# 2. Define the output path and save the summary file to Google Drive.
output_file_path = "/content/drive/MyDrive/engagement_summary.csv"
summary_pd.to_csv(output_file_path, index=False)

print(f"Summary data exported to: {output_file_path}")

# 3. Stop the SparkSession to release resources.
spark.stop()

ขั้นตอนที่ 2: ออกแบบการทดลอง (Experiment Design)

หลังจากที่เราได้ข้อมูลที่พร้อมใช้งานจากขั้นตอนที่แล้ว คำถามสำคัญสองข้อที่เกิดขึ้นก่อนที่เราจะวิเคราะห์ผลลัพธ์ก็คือ:

1. เราจะวัดผล “ความสำเร็จ” ของการทดลองนี้อย่างไร? ผลลัพธ์ต้องดีขึ้นแค่ไหนถึงจะเรียกว่า “ดีกว่า”?
2. แล้วเราต้องใช้ คนในการทดลองนี้กลุ่มละกี่คน ถึงจะมั่นใจได้ว่าผลที่ออกมาไม่ใช่เรื่องบังเอิญ?

ขั้นตอน “Experiment Design” นี้จะช่วยให้เราตอบคำถามทั้งสองข้อได้อย่างเป็นระบบและมีหลักการทางสถิติรองรับครับ โดยเราจะใช้ Minimum Detectable Effect (MDE) เพื่อตอบคำถามข้อแรก และใช้ Power Analysis เพื่อตอบคำถามข้อที่สองครับ

2.1 กำหนด Minimum Detectable Effect – MDE (เป้าหมายทางธุรกิจ)

คำถามแรกที่ต้องตอบในทางธุรกิจคือ:

“ผลลัพธ์ต้องดีขึ้นอย่างน้อยแค่ไหน เราถึงจะมองว่ามัน ‘คุ้มค่า’ ที่จะลงมือทำ?”

คำตอบของคำถามนี้คือสิ่งที่เราเรียกว่า Minimum Detectable Effect (MDE) ครับ มันคือ “ขนาดของความแตกต่างที่เล็กที่สุดที่มีความหมายในทางธุรกิจ” หากผลลัพธ์ดีขึ้นน้อยกว่าค่านี้ ก็อาจไม่คุ้มกับต้นทุนหรือความซับซ้อนที่เพิ่มขึ้น

สมมติว่าทีมต้องใช้เวลา 1 เดือนในการสร้างระบบส่งข้อความแบบ Personalized ซึ่งมีต้นทุนด้านเวลาและทรัพยากร

ถ้าผลการทดลองออกมาว่าข้อความแบบใหม่นี้ช่วยเพิ่ม Engagement Rate ได้แค่ 0.01% ซึ่งน้อยมากๆ แม้ผลลัพธ์นี้อาจจะ “มีนัยสำคัญทางสถิติ” แต่ในทางธุรกิจแล้วมัน “ไม่คุ้มค่า” กับเวลา 1 เดือน วันที่เสียไป

ทีมจึงอาจจะตกลงกันว่า “ถ้าจะทำทั้งที อย่างน้อยต้องเห็น Engagement Rate เพิ่มขึ้น 0.5% ถึงจะยอมทำ” ซึ่งค่า 0.5% นี้เองก็คือ MDE ของเราครับ

มันคือเส้นแบ่งระหว่าง “ผลลัพธ์ที่น่าสนใจทางสถิติ” กับ “ผลลัพธ์ที่คุ้มค่าทางธุรกิจ” นั่นเอง

โดยในโปรเจกต์นี้ เราจะตั้งสมมติฐานว่าทีมการตลาดต้องการเห็น Engagement Rate เพิ่มขึ้นอย่างน้อย 0.5% เราจึงกำหนด MDE ไว้ที่ 0.005

2.2 การวิเคราะห์ Power Analysis

เมื่อเรามี MDE แล้ว คำถามต่อไปคือ:

“เราต้องใช้ผู้ใช้ในแต่ละกลุ่มอย่างน้อยกี่คน (Minimum Sample Size) เพื่อที่จะสามารถตรวจจับความแตกต่างที่ระดับ MDE นั้นได้อย่างน่าเชื่อถือ?”

Power Analysis คือเครื่องมือทางสถิติที่ช่วยตอบคำถามนี้ โดยเราจะใช้ค่าสำคัญ 3 ค่าในการคำนวณ:

• Baseline Rate: อัตราความสำเร็จของกลุ่มควบคุม (Generic) ซึ่งจากข้อมูลของเราคือ ~1.79%
• Alpha (α): โอกาสที่จะสรุปผิดว่าผลลัพธ์แตกต่างกัน โดยทั่วไปตั้งไว้ที่ 5% หรือ 0.05
• Power (1-β): โอกาสที่จะตรวจจับความแตกต่างได้ถูกต้อง ถ้ามันมีความแตกต่างอยู่จริง โดยทั่วไปตั้งไว้ที่ 80% หรือ 0.80

เราจะนำค่าเหล่านี้ไปเข้าสูตรใน Python เพื่อคำนวณหาขนาด Sample Size ที่ต้องการครับ

import numpy as np
from statsmodels.stats.power import zt_ind_solve_power
from statsmodels.stats.proportion import proportion_effectsize

# 1. Define Parameters for Power Analysis
baseline_rate = 0.0179  # Control group's rate from our data (~1.79%)
mde_absolute = 0.005    # Our MDE: an absolute increase of 0.5%
target_rate = baseline_rate + mde_absolute

alpha = 0.05  # Significance level
power = 0.80  # Desired power

# 2. Calculate Required Sample Size
effect_size = proportion_effectsize(target_rate, baseline_rate)

required_sample_size = zt_ind_solve_power(
    effect_size=effect_size,
    alpha=alpha,
    power=power,
    alternative='larger'  # One-tailed better
)

print(f"Baseline Rate: {baseline_rate:.2%}")
print(f"Minimum Detectable Effect (MDE): {mde_absolute:+.2%}")
print(f"Target Rate: {target_rate:.2%}")
print("-" * 30)
print(f"To reliably detect an absolute lift of {mde_absolute:+.2%},")
print(f"we would need a sample size of approximately {int(np.ceil(required_sample_size))} users per group.")

Output:

Baseline Rate: 1.79%
Minimum Detectable Effect (MDE): +0.50%
Target Rate: 2.29%
------------------------------
To reliably detect an absolute lift of +0.50%,
we would need a sample size of approximately 9848 users per group.

Power Analysis บอกเราว่า เราต้องการผู้ใช้ในแต่ละกลุ่มอย่างน้อย 9,848 คน เพื่อให้การทดลองของเรามีพลัง (Power) มากพอที่จะตรวจจับความแตกต่างที่ระดับ 0.5% ได้อย่างน่าเชื่อถือ

เมื่อเราย้อนกลับไปดูข้อมูลที่เรามี (กลุ่ม Generic มี ~23,000 คน และกลุ่ม Personalized มี ~560,000 คน) จะเห็นว่าขนาดของกลุ่มตัวอย่างของเรานั้น ใหญ่เกินพอ ทำให้เรามั่นใจได้ว่าการวิเคราะห์ในขั้นตอนต่อไปจะมีน้ำหนักและน่าเชื่อถือครับ

ในขั้นตอนต่อไป เราจะมาพิสูจน์ด้วยสถิติกันว่า lift ที่เราเห็นนั้น “ชนะ” MDE ที่ 0.5% หรือไม่ และที่สำคัญคือช่วงความเชื่อมั่น (Confidence Interval) ของมันก็ต้องเอาชนะ MDE ด้วยเช่นกัน

Note: Confidence Interval (CI) คือ “ช่วงของค่า lift ที่แท้จริงที่เป็นไปได้ ที่เรามั่นใจ 95%” (α = 0.05)ในกรณีการที่ CI ทั้งช่วงอยู่เหนือ MDE (เช่น CI คือ [+0.6%, +0.9%] และ MDE คือ +0.5%) เปรียบเสมือนการบอกว่า “ต่อให้ผลลัพธ์จริงจะเอนเอียงไปทางที่แย่ที่สุดที่เป็นไปได้ มันก็ยังดีกว่ามาตรฐานความคุ้มค่าที่เราตั้งไว้” มันจึงเป็นการยืนยันผลที่แข็งแกร่งที่สุด ทำให้เราตัดสินใจทางธุรกิจได้อย่างมั่นใจและมีความเสี่ยงต่ำครับ

กราฟ Power Curve นี้ ผมทำขึ้นมาเพิ่มเติมเพื่อแสดงให้เห็นความสัมพันธ์ระหว่าง:

• แกน X (Minimum Detectable Effect – MDE): ขนาดความแตกต่างที่เราต้องการตรวจจับ
• แกน Y (Required Sample Size): จำนวนผู้ใช้ที่ต้องมีในแต่ละกลุ่ม

จะเห็นได้ชัดเจนว่า ยิ่งเราต้องการตรวจจับความแตกต่างที่เล็กลงเท่าไหร่ (MDE น้อยลง) เราก็ยิ่งต้องการขนาดกลุ่มตัวอย่างที่ใหญ่ขึ้นแบบก้าวกระโดด

ขั้นตอนที่ 3: วิเคราะห์เชิงสถิติ (Statistical Analysis)

หลังจากที่เราออกแบบการทดลองและมั่นใจว่ามีขนาดกลุ่มตัวอย่างที่ใหญ่เพียงพอแล้ว ก็ถึงเวลาตัดสินผลการแข่งขันระหว่างข้อความสองรูปแบบครับ เราจะใช้สถิติเพื่อตอบคำถามที่ว่า: “ความแตกต่างของ Engagement Rate ที่เราเห็นนั้น เป็นของจริง หรือแค่โชคช่วย?”

3.1 Hypothesis Testing (Two-Proportion Z-test)

ในส่วนนี้ เราจะทำการทดสอบสมมติฐาน (Hypothesis Testing) โดยก่อนจะเริ่มคำนวณ เราต้องตั้งสมมติฐาน 2 อย่างที่ตรงข้ามกันก่อน:

• สมมติฐานหลัก (Null Hypothesis, H₀): คือสมมติฐานที่เราตั้งไว้ในตอนแรกว่า “ไม่มีอะไรเกิดขึ้น” หรือ “ไม่มีความแตกต่าง” ในกรณีนี้คือ อัตราการมีส่วนร่วม (Engagement Rate) ของกลุ่ม Personalized และกลุ่ม Generic ไม่มีความแตกต่างกัน ความแตกต่างใดๆ ที่เราเห็นเป็นเพียงเรื่องบังเอิญทางสถิติ
• สมมติฐานรอง(Alternative Hypothesis, H₁): คือสิ่งที่ตรงข้ามกับสมมติฐานหลัก และเป็นสิ่งที่เราต้องการจะพิสูจน์ ในกรณีนี้คือ อัตราการมีส่วนร่วมของทั้งสองกลุ่มมีความแตกต่างกันอย่างมีนัยสำคัญ

เมื่อเขียนเป็นสมการ จะสามารถเขียน 2 สมมติฐานได้ดังนี้:

H₀: Engagement Rate (Personalized) = Engagement Rate (Generic)
H₁: Engagement Rate (Personalized) ≠ Engagement Rate (Generic)

เป้าหมายของเราคือการดูว่าเรามีหลักฐานทางสถิติที่หนักแน่นพอที่จะ “ปฏิเสธสมมติฐานหลัก (Reject H₀)” ได้หรือไม่ โดยเครื่องมือที่เราจะใช้คือ Two-Proportion Z-test เพื่อคำนวณหาค่า p-value

• p-value คืออะไร? คือความน่าจะเป็นที่จะสังเกตเห็นผลลัพธ์ที่แตกต่างกันขนาดนี้ (หรือมากกว่านี้) หากสมมติว่าสมมติฐานว่าง (H₀) เป็นเรื่องจริง
• โดยถ้า p-value ที่ได้มีค่าน้อยมาก (โดยทั่วไปคือน้อยกว่า 0.05) ก็แปลว่ามันไม่น่าจะใช่เรื่องบังเอิญ เราจึงมีเหตุผลเพียงพอที่จะ “ปฏิเสธ H₀” และหันไปยอมรับ H₁ แทน

import pandas as pd
import numpy as np
from statsmodels.stats.proportion import proportions_ztest

# 1. Load the summary data we prepared in Step 1
file_path = "/content/drive/MyDrive/engagement_summary.csv"
summary_df = pd.read_csv(file_path)
print("Summary data loaded successfully:")
print(summary_df)

# 2. Prepare data for the Z-test
# count: Number of successes (engaged users) in each group.
# nobs: Number of observations (total users) in each group.
count = summary_df['n_engaged']
nobs = summary_df['n_users']

# 3. Perform the two-proportion z-test
z_stat, p_value = proportions_ztest(count=count, nobs=nobs, alternative='two-sided')

print("\n--- Z-test Results ---")
print(f"Z-statistic: {z_stat:.20f}")
print(f"P-value: {p_value:.20f}")

Output:

Summary data loaded successfully:
   message_type  n_users  n_engaged  engagement_rate
0  Personalized   564577      14423         0.025547
1       Generic    23524        420         0.017854

--- Z-test Results ---
Z-statistic: 7.37007812654541449859
P-value: 0.00000000000017052807

p-value ที่ได้คือ 1.7e-13 ซึ่งเป็นตัวเลขที่น้อยมากๆ และน้อยกว่าเกณฑ์ 0.05 ของเราอย่างเทียบไม่ติด นี่คือหลักฐานที่หนักแน่นว่า ความแตกต่างของ Engagement Rate ระหว่างสองกลุ่มนั้นเป็นของจริง และมีนัยสำคัญทางสถิติ ครับ

3.2 Confidence Interval (CI)

จากข้อมูลที่เรามี เราคำนวณ Absolute Lift (ผลต่างของ Engagement Rate) ได้ที่ +0.77% แต่นี่เป็นเพียงผลลัพธ์ที่เกิดขึ้นใน “กลุ่มตัวอย่าง” ของเราเท่านั้น

คำถามที่สำคัญคือ ถ้าเราทำการทดลองนี้กับประชากรทั้งหมด หรือสุ่มกลุ่มตัวอย่างมาใหม่ “ค่า lift ที่แท้จริง” จะยังเป็น +0.77% อยู่หรือไม่ หรือจะเหวี่ยงไปอยู่ที่ค่าอื่น?

นี่คือจุดที่ ช่วงความเชื่อมั่น (Confidence Interval – CI) เข้ามามีบทบาทครับ CI จะให้ “ช่วงของค่าที่เป็นไปได้” สำหรับ lift ที่แท้จริง โดยเรามั่นใจ 95% ว่าค่าจริงจะตกอยู่ในช่วงนี้

และที่สำคัญยิ่งกว่านั้น คือการนำช่วง CI นี้ไปเทียบกับ MDE ที่เราตั้งไว้ครับ หาก CI ทั้งช่วงอยู่สูงกว่า MDE (ในกรณีนี้คือ +0.5%) ก็จะเป็นการยืนยันว่า ต่อให้ผลลัพธ์จริงจะเอนเอียงไปทางค่าต่ำสุดของช่วงที่เรามั่นใจ มันก็ยังคง “คุ้มค่า” ในทางธุรกิจอยู่ดี ซึ่งหมายถึงความเสี่ยงที่ต่ำในการตัดสินใจครับ

# 1. Get the rates for each group
rate_generic = summary_df.loc[summary_df['message_type'] == 'Generic', 'engagement_rate'].iloc[0]
rate_personalized = summary_df.loc[summary_df['message_type'] == 'Personalized', 'engagement_rate'].iloc[0]

# 2. Calculate the observed lift
absolute_lift = rate_personalized - rate_generic

# 3. Calculate the 95% Confidence Interval for the lift
n_personalized = summary_df.loc[summary_df['message_type'] == 'Personalized', 'n_users'].iloc[0]
n_generic = summary_df.loc[summary_df['message_type'] == 'Generic', 'n_users'].iloc[0]

std_err_diff = np.sqrt((rate_personalized * (1 - rate_personalized) / n_personalized) + \
                      (rate_generic * (1 - rate_generic) / n_generic))

# z-score for 95% confidence is 1.96
margin_of_error = 1.96 * std_err_diff
ci_low = absolute_lift - margin_of_error
ci_high = absolute_lift + margin_of_error

print(f"Absolute Lift: {absolute_lift:+.4f} or {absolute_lift:+.2%}")
print(f"95% Confidence Interval (CI): [{ci_low:+.4f}, {ci_high:+.4f}]")
print(f"Which means the true lift is likely between {ci_low:+.2%} and {ci_high:+.2%}")

Output:

Absolute Lift: +0.0077 or +0.77%
95% Confidence Interval (CI): [+0.0060, +0.0094]
Which means the true lift is likely between +0.60% and +0.94%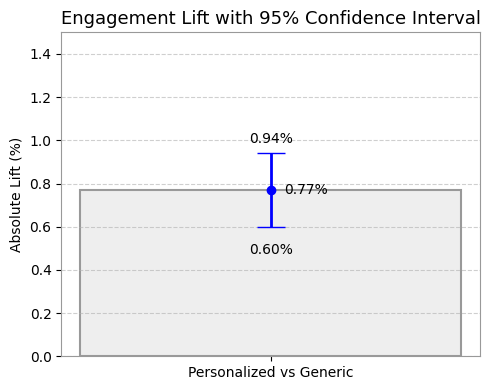

ผลลัพธ์นี้บอกเราว่า เรามั่นใจ 95% ว่าการเปลี่ยนไปใช้ Personalized Message จะช่วยเพิ่ม Engagement Rate ได้ อย่างน้อย +0.60% และอาจจะสูงได้ถึง +0.94%

ขั้นตอนที่ 4: สรุปผลเชิงธุรกิจ (Business Conclusion)

หลังจากที่เราผ่านขั้นตอนทางเทคนิคและการวิเคราะห์ทางสถิติมาทั้งหมด ก็ถึงเวลาที่จะนำตัวเลขเหล่านั้นมาสรุปเชิงธุรกิจ และให้คำแนะนำที่ชัดเจนเพื่อการตัดสินใจครับ

4.1 การตอบคำถามทางธุรกิจ

จากคำถามหลักที่ว่า “การส่งข้อความแบบ Personalized ช่วยเพิ่ม Engagement ได้จริงและคุ้มค่าที่จะทำหรือไม่?”

คำตอบคือ: “จริงและคุ้มค่าอย่างยิ่ง” ครับ เราสามารถสรุปได้อย่างมั่นใจโดยมีเหตุผล 3 ข้อที่สนับสนุนดังนี้ครับ:

1. ผลลัพธ์มีนัยสำคัญทางสถิติ (Statistically Significant): p-value ที่ต่ำมากยืนยันว่า Lift ที่เพิ่มขึ้น +0.77% นั้นเป็นของจริง ไม่ใช่เรื่องบังเอิญ
2. ผลลัพธ์มีนัยสำคัญทางธุรกิจ (Business Relevant): Lift ที่ +0.77% นั้น สูงกว่าเกณฑ์ความคุ้มค่า (MDE) ที่เราตั้งไว้ที่ +0.50% อย่างชัดเจน
3. ผลลัพธ์มีความเสี่ยงต่ำ (Low Risk): นี่คือจุดที่สำคัญที่สุด! ช่วงความเชื่อมั่นทั้งช่วง [+0.60%, +0.94%] อยู่สูงกว่า MDE ทั้งหมด ซึ่งเป็นการบอกว่าต่อให้ผลลัพธ์จริงจะออกมาแย่ที่สุดเท่าที่เป็นไปได้ มันก็ยังคง “คุ้มค่า” ที่จะทำอยู่ดี

สรุปได้ว่า ควรเดินหน้าแคมเปญ Personalized Messaging ในสเกลที่ใหญ่ขึ้นได้เลยครับ

Project นี้ เราได้ผ่านกระบวนการ A/B Testing ตั้งแต่ต้นจนจบ ตั้งแต่การใช้ PySpark เตรียมข้อมูลขนาดใหญ่, การออกแบบการทดลองด้วย MDE และ Power Analysis, ไปจนถึงการพิสูจน์ผลลัพธ์ด้วย Z-test และ Confidence Intervals

ทั้งหมดนี้แสดงให้เห็นว่าเราสามารถใช้ข้อมูลและสถิติในการตัดสินใจทางธุรกิจได้อย่างมั่นใจ เพื่อลดการคาดเดาและสร้างผลกระทบที่วัดผลได้จริง แต่หัวใจสำคัญที่อยากฝากไว้คือ แม้ผลลัพธ์จะมี “นัยสำคัญทางสถิติ” แต่คำถามที่ต้องตอบควบคู่กันไปเสมอคือ มันมี “นัยสำคัญทางธุรกิจ” หรือคุ้มค่าพอที่จะลงมือทำจริงหรือไม่

ขอบคุณทุกคนที่ติดตามอ่านมาจนจบนะครับ! สำหรับใครที่อยากดู code การทำงานทั้งหมด สามารถเข้าไปดูได้ที่ ลิงก์ GitHub และหากมีคำถามหรืออยากแลกเปลี่ยนไอเดีย สามารถติดต่อเข้ามาได้เลยนะครับ 😊🤍